Credit: Planck collaboration (2015)
In January, NYU Abu Dhabi hosted the Conference on the Foundations of Cosmology and Quantum Gravity, a three-day workshop that brought together philosophers and physicists to discuss theories of quantum gravity and how cosmology can provide tests of candidate theories. One major testing ground for theories of quantum gravity is the early universe, where energy densities, and therefore curvature, would have been very high. The current “standard model” of cosmology—the ΛCDM model—is supplemented with a period of inflation to account for the surprising uniformity of temperature in the cosmic microwave background. Though physicists widely accept inflation, various talks at the Abu Dhabi conference called into question its uniqueness and explanatory power.
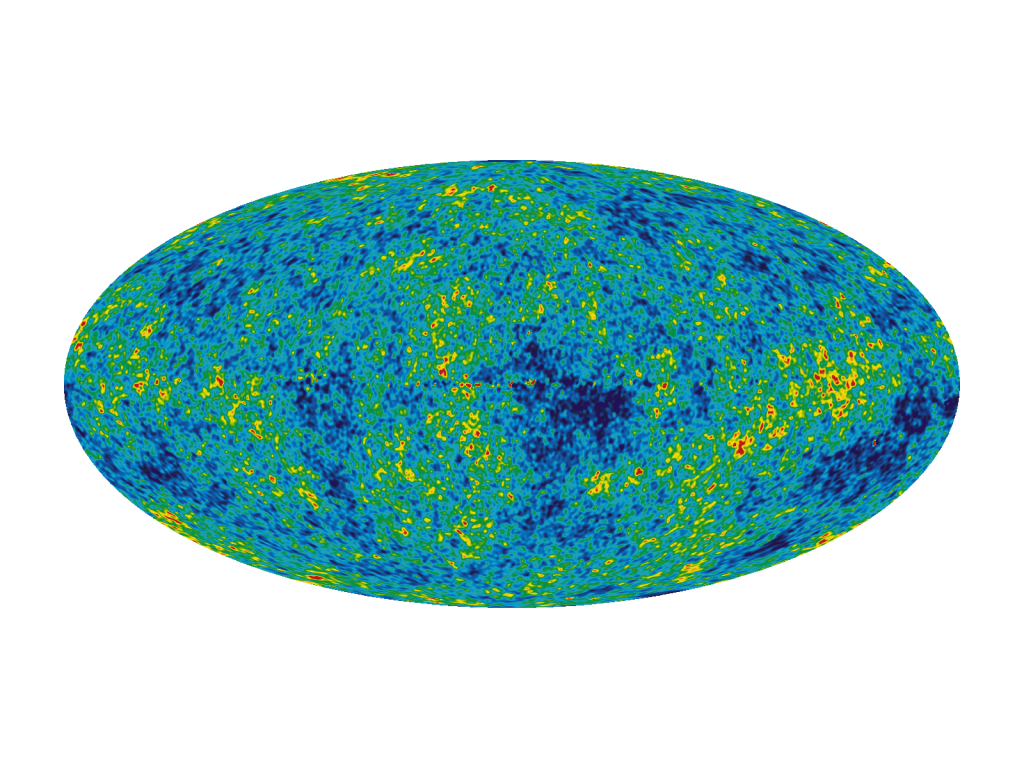
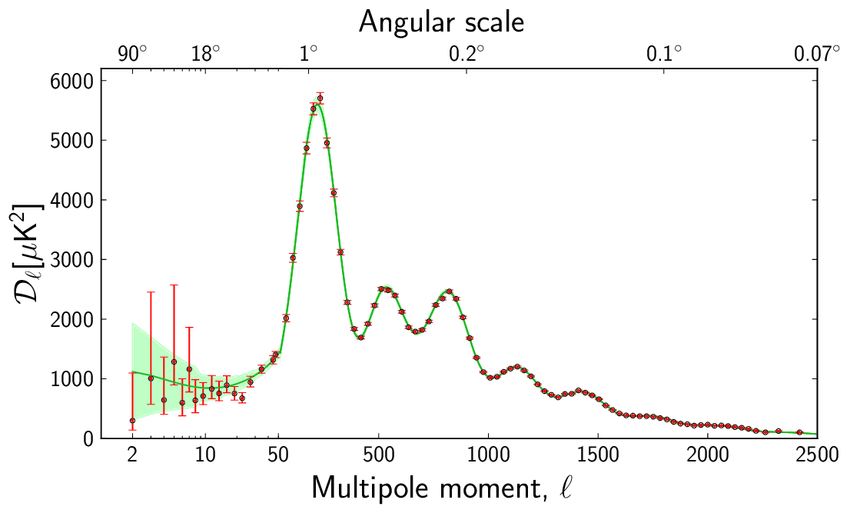
Our best evidential window into the early universe is the cosmic microwave background (CMB), which is a relic of the oldest electromagnetic radiation existing in the universe. Early observations of the CMB indicated that the temperature of the radiation was isotropic—the same at all angles of the sky—and equal to about 2.725K. After nine years, WMAP data showed very slight anisotropies in the temperature distribution of the CMB (about 1 part in 10,000), and more recent data from Planck shows that the power spectrum of anisotrpies takes on a very distinct shape.
Inflation has been successfully used to understand the remarkable uniformity of the CMB, as well as the power spectrum of the small anisotropies. As such, it is widely accepted as an essential addition to the ΛCDM model of cosmology. For the former, physicists invoke inflation as a solution to the horizon and flatness problems, while the latter requires inflation with linear perturbation theory. I will discuss the horizon problem and the anisotropies in the CMB, since the flatness problem requires more background about the observed state of our universe.
The extreme uniformity of the CMB raises the horizon problem for ΛCDM. The size and extreme uniformity of the universe at the time of the CMB (known of the surface of last scattering, approximately 380,000 years after the big bang) raises concerns for the ordinary expanding universe. If the universe expands at a rate consistent with the current epoch, then distant regions in the CMB would not have been in causal contact with one another at any point in the past history of the universe. The near exact thermal equilibrium of distant regions then seems exceedingly unlikely. Inflation solves the horizon problem by postulating a new phase of exponential expansion of spacetime; distant regions would have been much closer together before the onset of inflation, and would therefore be able to be in causal contact. This helps to explain the near thermal equilibrium of distant regions in the CMB.
Crucially for the prospects of structure formation in the early universe, the CMB radiation is not in exact thermal equilibrium. As the WMAP image shows, there are small deviations from complete uniformity of temperature. These slight anisotropies in the CMB correspond to inhomogeneities in the matter and radiation density at the surface of last scattering. Without slight deviations from exact homogeneity, large scale structures like stars, planets, galaxies, and galactic clusters would not have formed in the post-inflationary epoch. Inflation explains the presence, size, and distribution of the observed anisotropies with a supplemental linear perturbation theory. Roughly, one assumes that the universe near the start of inflation is a vacuum. In quantum theory, “vacuum fluctuations” are possible: this means that occasionally particle-antiparticle pairs will be spontaneously created from the vacuum, and may then recombine and annihilate one another. These particle pairs have a complementary wave description, and this is used in linear perturbation theory. A vacuum excitation associated with a particular wavelength will have that wavelength rapidly increase during inflation. At some point the wavelengths will get so big that they extend beyond the Hubble radius. When this happens, those fluctuations become standing waves, and the resulting power spectrum of fluctuations matches the data shown in the graph above. So, not only does inflation solve some conceptual problem with the standard big bang model, but it also manages to predict the distribution of observed anisotropies in the CMB. Inflation thus seems like an empirically successful, perhaps conceptually necessary addition to ΛCDM.
One question that has often arisen in debates in the philosophy of science concerns the uniqueness of a successful model or theory. If one is to be a scientific realist, there must be some convincing argument that other, equally well-motivated models cannot reproduce the same successful predictions. In many cases this worry arises only in principle, since no serious rivals to a theory are currently in play. Where alternative models exist, they may be deemed as ad hoc, or conceptually incompatible with other successful models within the discipline. However, there exist serious alternatives to inflation that are at present equally well-motivated by fundamental theory.
In his talk, Professor Robert Brandenberger highlighted that the necessary ingredients for predicting the power spectrum of anisotropies in the CMB (as well as other important cosmological phenomena, such as the power spectrum of galaxy distribution and baryon acoustic oscillations) existed before being adapted to inflation. These predictions are therefore not unique to inflation. Additionally, alternative models like a bouncing universe model, or a model in which the universe emerges from some non-spatiotemporal “initial” state, can solve the flatness and horizon problems. So there exist serious classes of competitors to inflation, at least in terms of reproducing its empirical and conceptual successes.
Does inflation gain the upper hand by fitting better with the existing conceptual foundations in fundamental physics? Even here, it’s not clear that inflation is the better option. In the 1980s, physicists had a set of preferred approaches to unifying the fundamental forces into a new theory. These were known as Grand Unified Theories (GUTs) or supersymmetry (SUSY) models. Inflation fit well with these types of theories, and therefore inflation seemed to fit with best with the conceptual foundations of emerging physics. Now, however, data from particle accelerators has all but ruled out GUTs and SUSY, and inflation is a model in search of an underlying framework. Bounce models fit well with an approach to quantum gravity called loop quantum cosmology, while emergent universe solutions are favoured by certain cosmological models informed by string theory. Given that loop quantum gravity and string theory are two of the most favoured frameworks for quantum gravity, these alternatives might even be said to fit better with existing conceptual foundations in fundamental physics.
To sum up, I will answer the title question of this post. Does cosmology need inflation? No. Cosmology needs a mechanism to explain the observed galaxy distribution and corresponding anisotropies in the CMB. The ΛCDM model of cosmology also needs a convincing explanation for conceptual problems like the horizon and flatness problems. Inflation is one candidate solution, which has been around the longest. But perhaps alternatives could be favoured as pointing the way to a theory of quantum gravity.
Image credit: WMAP data and power spectrum: NINE YEAR MICROWAVE SKY . NASA / WMAP Science Team WMAP # 121238 (2012)
[…] in the early universe, also known as inflation, as a possible explanation for these two issues. In his blog post, Adam Koberinski argues that we need not posit inflation to account for the above two issues; […]