
by: Helen Meskhidze and Jingyi Wu
ΛCDM, the “standard model” of cosmology, is thought to face two issues: the horizon problem and the flatness problem. Cosmologists supplement ΛCDM with a period of rapid expansion in the early universe, also known as inflation, as a possible explanation for these two issues. In his blog post, Adam Koberinski argues that we need not posit inflation to account for the above two issues; relatedly, in the cosmology community, there has been a debate on whether cosmology needs inflation (originally between Ijjan, Steinhardt & Loeb (2013) and Guth, Kaiser & Nakamura (2013) but since expanded to include many more). Richard Dawid takes the debate to reflect a bigger question about what it means for a theory to be confirmed, especially when the theory is underdetermined (i.e., the empirical data available does not lead us to a single theory as it may be compatible with multiple rival theories). At the Foundations of Cosmology and Quantum Gravity conference in Abu Dhabi in January 2020, Dawid used inflationary cosmology as a case study for introducing meta-empirical criteria of assessment which might serve to guide us when confronting issues of underdetermination. In the following blog post, we evaluate his general argument for these meta-empirical considerations in theory assessment.
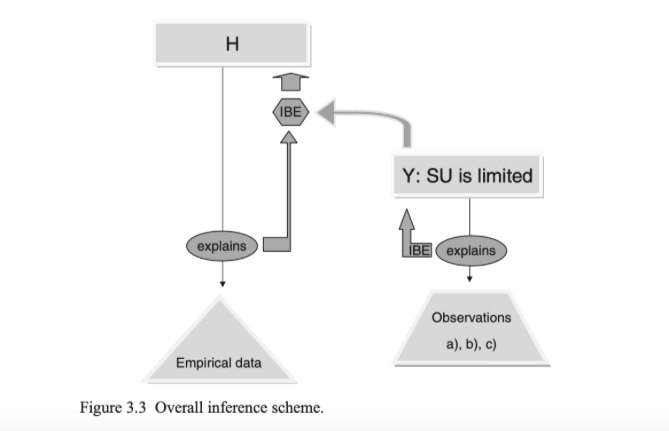
In his paper “Delimiting the Unconceived” (2018), Dawid discusses the link between meta-empirical considerations and underdetermination. We take him to be addressing the following question: “Given that our empirical data are compatible with multiple theories, some of which might not yet be conceived, how can we endorse our current theories?” Or, more simply, “How can we trust our current theories?” He provides a two-part answer, which he casts in a Bayesian confirmation framework (see Figure below for the overall inference scheme):
For Dawid, there are three main arguments for non-empirical confirmation: the no alternatives argument (NAA; that despite extensive searching, researchers have not found any alternatives to the current theory), the meta-inductive argument (MIA; that theories in the research field that exhibit a given set of conditions have shown a tendency to being viable/successful in the past), and the unexpected explanatory interconnections argument (UEA; that a theory explains something novel, something it was not designed to explain).
Dawid (2013, P68)
The first step in Dawid’s argument is to claim that when we are in a situation in which NAA, MIA and UEA all hold, by inference to the best explanation (IBE), we can infer that the theory space is severely constrained.
The second step is to use IBE to confirm our current theory: given the fact that the theory space is severely constrained, our current theory is the best explanation for the empirical data.
Dawid applies these arguments to string theory and inflationary cosmology, claiming that NAA, MIA, and UEA apply to both situations. He then uses the above two-step argument to first suggest that we have meta-empirical reasons to constrain the theory space, and then claim that string theory and inflationary cosmology are confirmed.
There is far from a consensus however as to whether NAA, MIA, and UEA ever hold in scientific practice in general, and in string theory or inflationary cosmology in particular. Daniele Oriti, another keynote speaker at the Foundations of Cosmology and Quantum Gravity conference, gives a general critique of these conditions in a 2017 paper. There have also been alternatives proposed to inflation, suggesting that NAA might not apply to inflationary cosmology. For examples of alternatives that resolve the horizon problem, see Albrecht and Magueijo’s 1999 proposal to vary the speed of light as well as Bessada, Kinney, Stojkovic and Wang’s 2009 proposal for tachyacoustic cosmology (see Brandenberger 2009 for a broader review of some alternatives). Though one might insist that viable alternatives to inflation ought to resolve both the horizon and flatness problems at once, we are skeptical that such an argument can be made. In particular, it seems like the NAA applies only if we set the standards of alternatives to those that solve both the horizon and flatness problems. But It is unclear whether we have good reasons to set the standards for alternatives so high. Indeed, demanding that every viable alternative solve both problems simultaneously seems to implicitly require that the UEA be satisfied in each case. However, why UEA should apply in each case demands independent justifications.
Furthermore, it is not clear that the IBEs in Dawid’s two-step argument are well justified. With respect to the first IBE, we are skeptical that not having any alternatives to our current theory puts a constraint on the entire theory space. In other words, having no alternatives would at best suggest that the theory space that we have already explored is limited; it would not, however, mean that there are constraints on unconceived alternatives.
With regard to the second IBE, Earman (Chapter 5, 1995) questions whether the horizon problem is sufficiently well-posed, i.e., whether it is the kind of problem that needs an explanation at all. This suggests that the second IBE might not be very well motivated. At the very least, we should be clearer on when we would demand an explanation and what form these explanations should take.
Acknowledgment: We’d like to thank David Freeborn for discussing some of the materials in the above post with us as well as Chris Smeenk and Jim Weatherall for their suggestions with respect to alternatives to inflation.